4.1 循环神经网络

学习目标

目标
- 了解序列模型相关概念
- 掌握循环神经网络原理
应用
- 应用RNN原理手写一个RNN的前向和反向传播过程

4.1.1 序列模型

4.1.1.1 定义

通常在自然语言、音频、视频以及其它序列数据的模型。

催生了自然语言理解、语音识别、音乐合成、聊天机器人、机器翻译等领域的诸多应用。

4.1.1.2 类型

语音识别，输入一段语音输出对应的文字

情感分类，输入一段表示用户情感的文字，输出情感类别或者评分

机器翻译，两种语言的互相翻译

4.1.1.3 为什么在序列模型使用CNN等神经网络效果不好

序列数据前后之间是有很强的关联性
- 如：曾经有一份真挚的感情,摆在我面前,我没有去?_
序列数据的输入输出长度不固定

4.1.2 循环神经网络

循环(递归)神经网络（RNN）是神经网络的一种。RNN将状态在自身网络中循环传递，可以接受时间序列结构输入。

4.1.2.1 类型

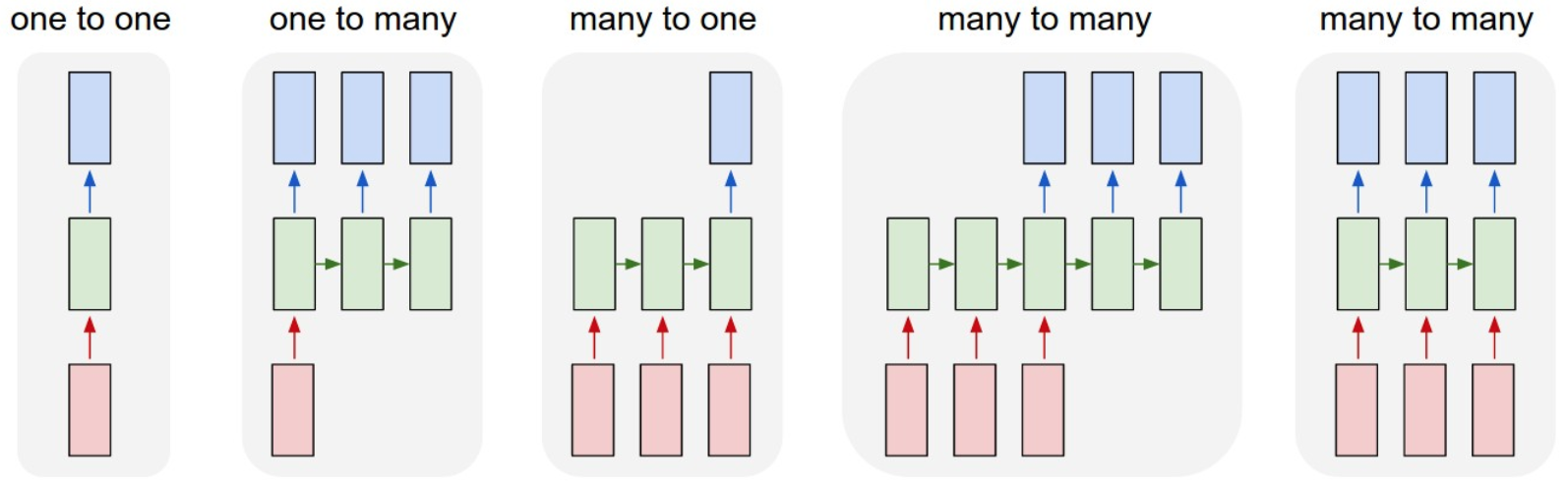
一对一：固定的输入到输出，如图像分类
一对多：固定的输入到序列输出，如图像的文字描述
多对一：序列输入到输出，如情感分析，分类正面负面情绪
多对多：序列输入到序列的输出，如机器翻译,称之为编解码网络
同步多对多：同步序列输入到同步输出，如文本生成，视频每一帧的分类，也称之为序列生成

这是循环神经网络的一些结构以及场景，那么我们接下来以基础的一种结构来看具体RNN怎么做的？

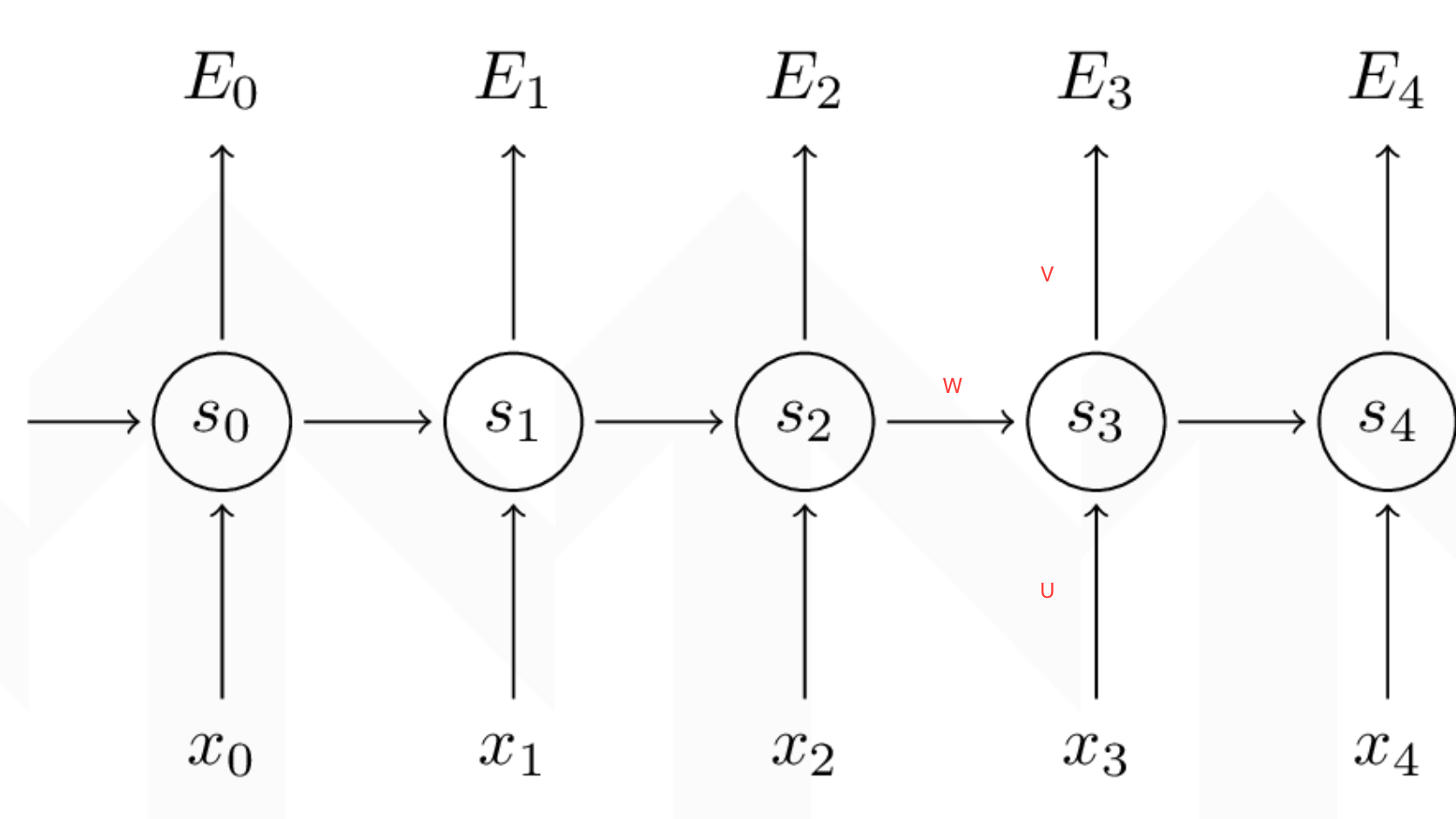
4.1.2.2 基础循环网络介绍

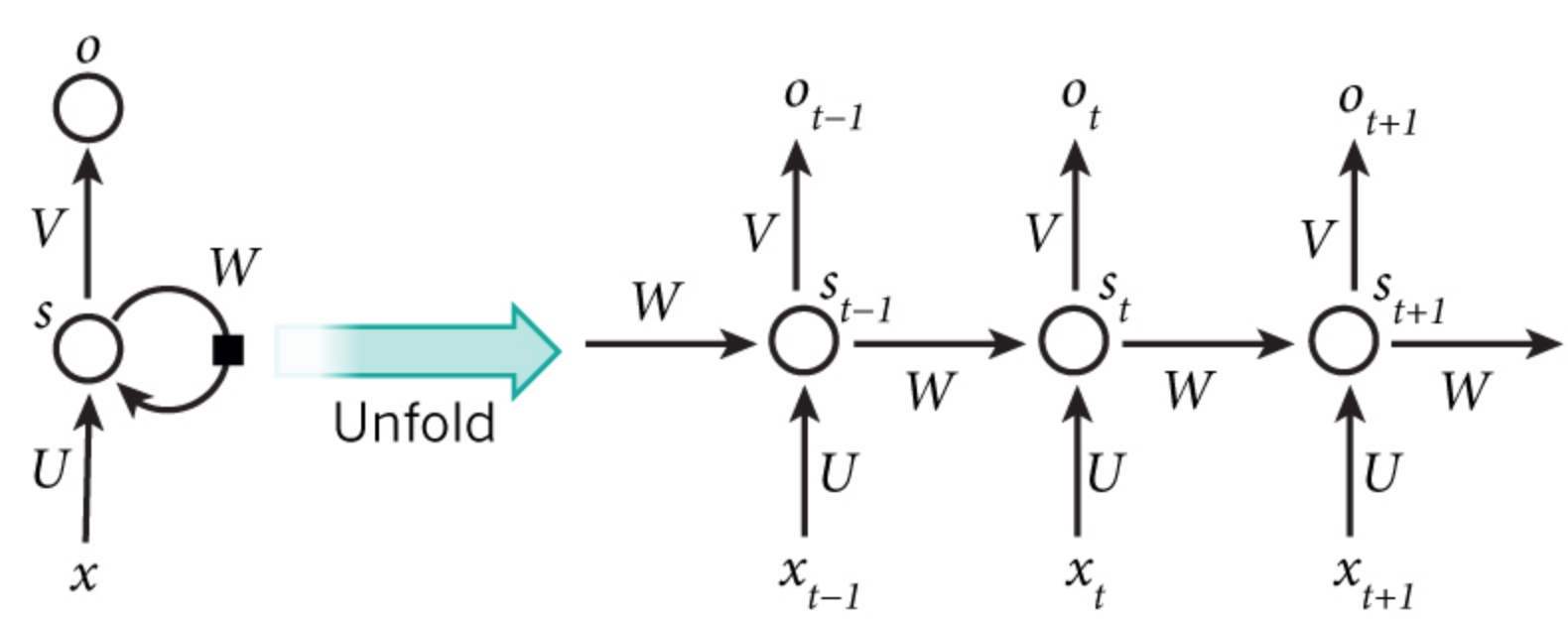
$x_t$ :表示每一个时刻的输入
$o_t$ :表示每一个时刻的输出
$s_t$ :表示每一个隐层的输出
中间的小圆圈代表隐藏层的一个unit(单元)
所有单元的参数共享

通用公式表示：

$s_0=0$
$s_{t} = g1(Ux_t + Ws_{t-1} + b_{a})$
$o_{t} = g2(V{s_t}+b_{y})$

$g1,g2$ :表示激活函数，g1:tanh/relu, g2:sigmoid、softmax其中如果将公式展开：

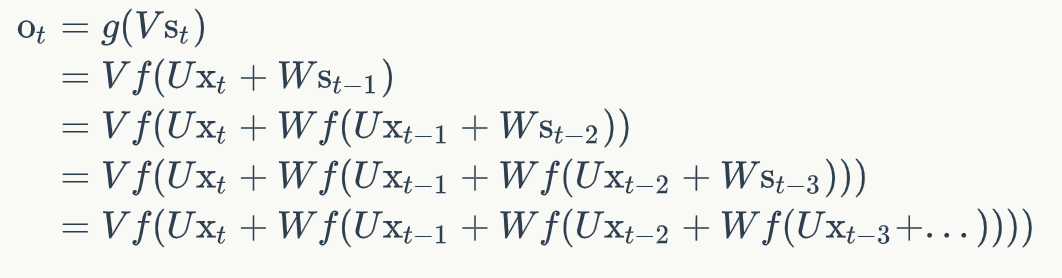
循环神经网络的输出值 $o_t$ ，是受前面历次输入值 $x_{t-1},x_{t},x_{t+1}$ 影响。

4.1.2.3 序列生成案例

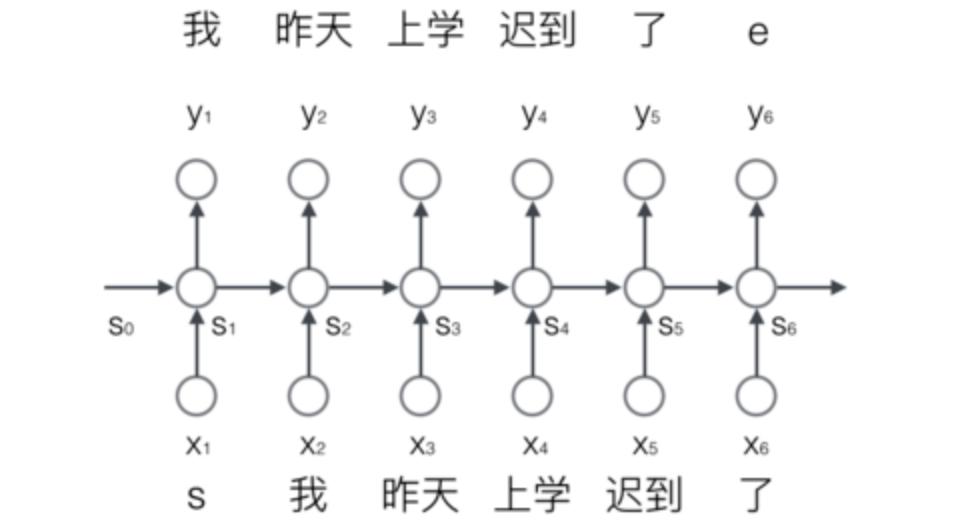
通常对于整个序列给一个开始和结束标志，start,end标志。

s 我昨天上学迟到了 e

输入到网络当中的是一个个的分词结果，每一个词的输入是一个时刻。

4.1.2.4 词的表示

为了能够让整个网络能够理解我们的输入（英文/中文等），需要将词进行用向量表示。

建立一个包含所有序列词的词典包含（开始和标志的两个特殊词，以及没有出现过的词用等），每个词在词典里面有一个唯一的编号。
任意一个词都可以用一个N维的one-hot向量来表示。其中，N是词典中包含的词的个数

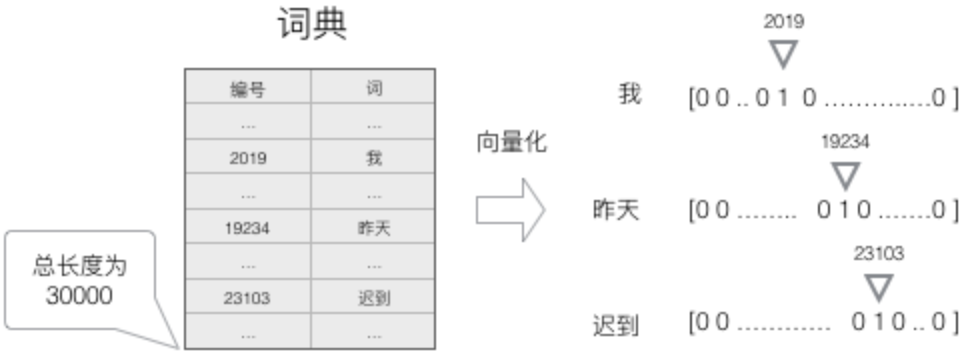
我们就得到了一个高维、稀疏的向量（稀疏是指绝大部分元素的值都是0）。

4.1.2.4 输出的表示-softmax

RNN这种模型，每一个时刻的输出是下一个最可能的词，可以用概率表示，总长度为词的总数长度：

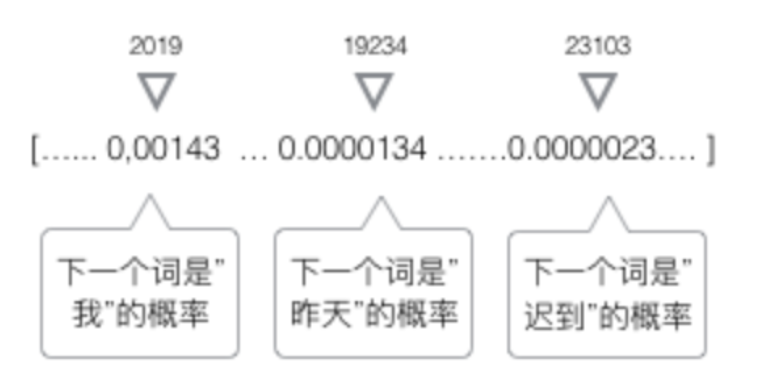
每一个时刻的输出 $s_t$ 都是词的总数长度，接上softmax回归即可。

4.1.2.5 矩阵运算表示

假设以上面的例子：对于网络当中某一时刻的公式中

1、 $\mathrm{s}_t=relu(U\mathrm{x}_t+W\mathrm{s}_{t-1})$

2、 $o_{t} = softmax(V{s_t})$

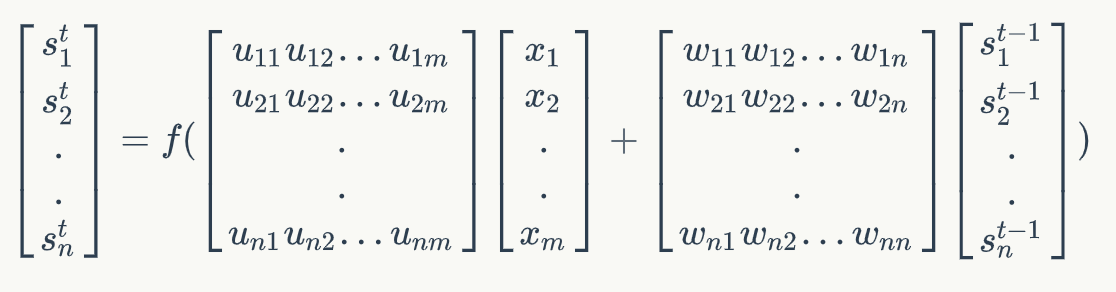
1、形状表示:[n, m] x [m, 1] +[n, n] x [n, 1] = [n, 1]
- 则矩阵U的维度是n x m，矩阵W的维度是n x n
- m：词的个数，n：为输出s的维度

注:此步骤可以简化：[u,w] x [ $\frac{x}{s}$ ] = [n, n+m] x [n +m, 1] = [n, 1]

2、形状表示：[m, n] x [n, 1] = [m, 1]
- 矩阵V维度：[m, n]

总结：其中的 $n$ 是可以人为去进行设置。

4.1.2.6 交叉熵损失

总损失定义：

一整个序列（一个句子）作为一个训练实例，总误差就是各个时刻词的误差之和。

$E_{t}(y_{t},\hat{y_{t}}) = -y_{t}log(\hat{y_{t}})$

$E(y,\hat{y}) = \sum_{t}E_{t}(y_{t},\hat{y_{t}})=-\sum_{t}y_{t}log(\hat{y_{t}})$

在这里， $y_t$ 是时刻 t 上正确的词， $\hat y_{t}$ 是预测出来的词

4.1.2.7 时序反向传播算法(BPTT)（重要）

对于RNN来说有一个时间概念，需要把梯度沿时间通道传播的 BP 算法，所以称为Back Propagation Through Time-BPTT

我们的目标是计算误差关于参数U、V和W以及两个偏置bx,by的梯度，然后使用梯度下降法学习出好的参数。由于这三组参数是共享的，我们需要将一个训练实例在每时刻的梯度相加。

1、要求：每个时间的梯度都计算出来t=0,t=1,t=2,t=3,t=4，然后加起来的梯度, 为每次W更新的梯度值。
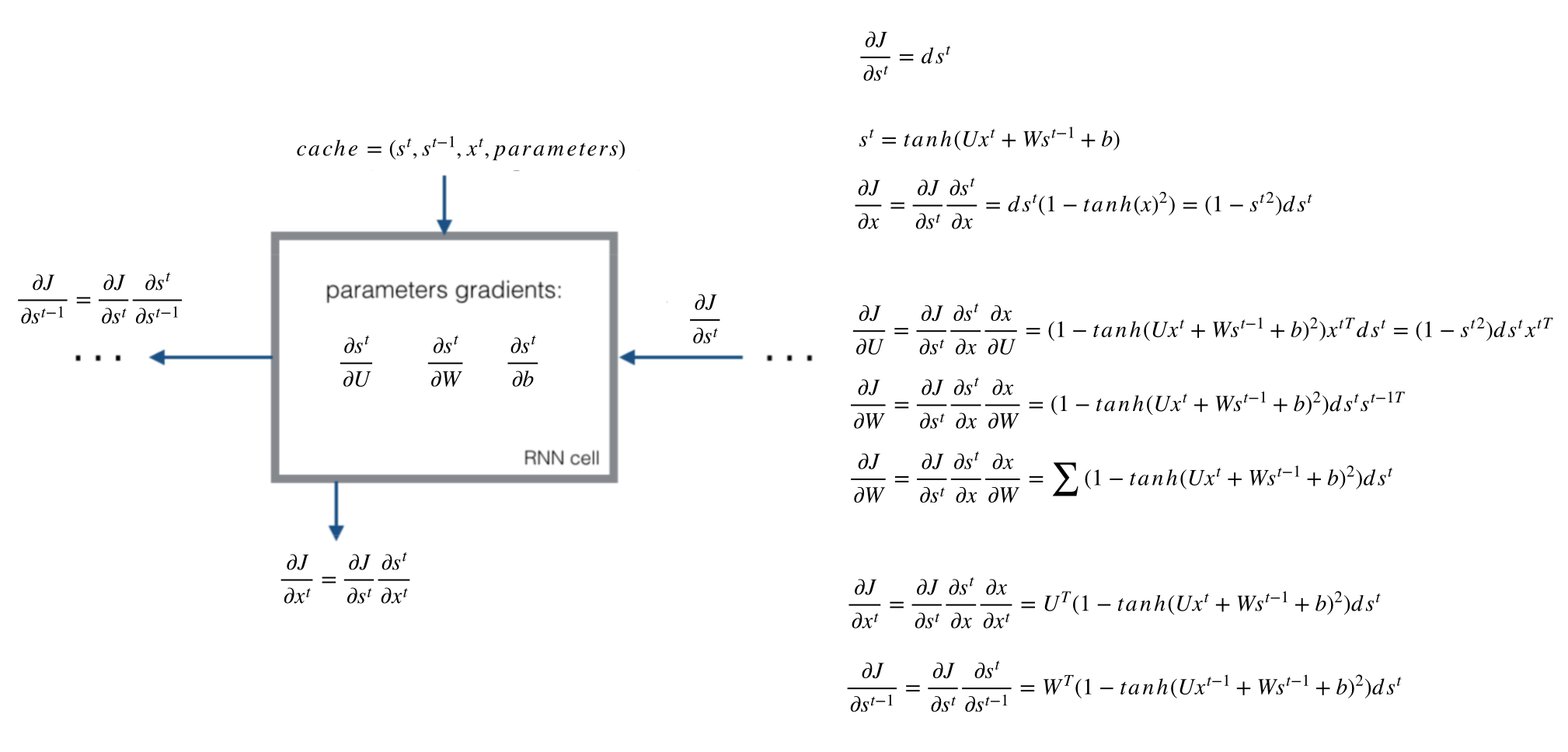
2、求不同参数的导数步骤：
- 最后一个cell:
  - 计算最后一个时刻交叉熵损失对于s_t的梯度，记忆交叉熵损失对于s^t,V,by的导数
  - 按照图中顺序计算
- 最后一个前面的cell:
  - 第一步：求出当前层损失对于当前隐层状态输出值 $s^{t}$ 的梯度 $+$ 上一层相对于 $s^{t}$ 的损失
  - 第二步：计算tanh激活函数的导数
  - 第三步：计算 $Ux_t + Ws_{t-1} + b_{a}$ 的对于不同参数的导数

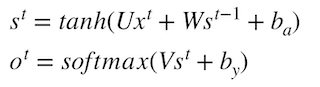
4.1.2.8 梯度消失与梯度爆炸

由于RNN当中也存在链式求导规则，并且其中序列的长度位置。所以

如果矩阵中有非常小的值，并且经过矩阵相乘N次之后，梯度值快速的以指数形式收缩，较远的时刻梯度变为0。
如果矩阵的值非常大，就会出现梯度爆炸

4.1.3 RNN 总结

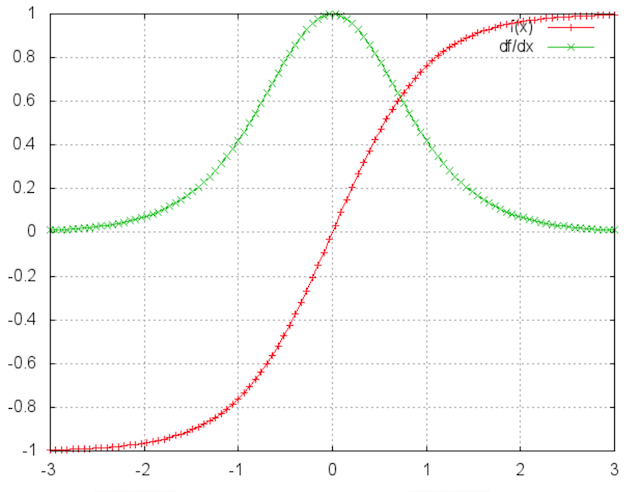
总结使用tanh激活函数。

完整计算流程

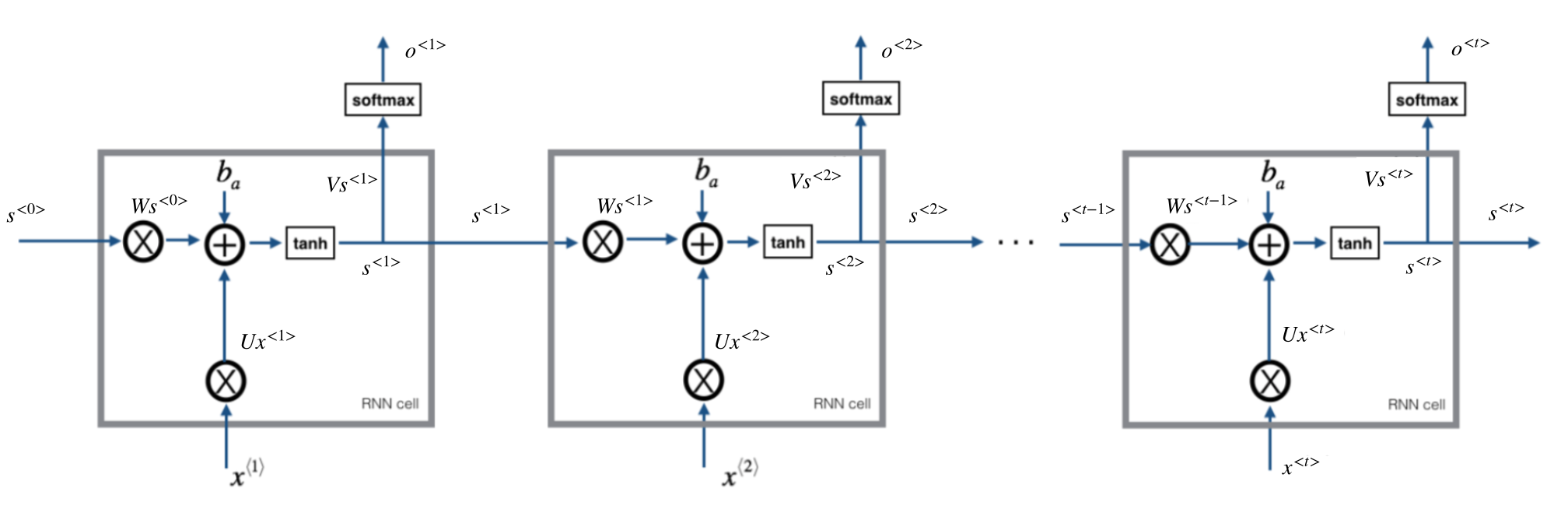
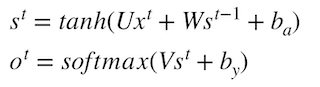
反向传播过程结果

4.1.4 案例：手写一个RNN的前向传播以及反向传播

4.1.4.1 案例演示

4.1.4.2 流程

前向传播过程
- 单个cell的前向传播
- 所有cell的前向传播
反向传播过程

4.1.4.3 代码案例

1、前向传播过程

根据前向传播的公式来进行编写:

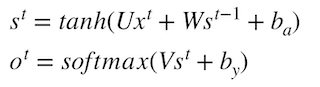
def rnn_cell_forward(x_t, s_prev, parameters):
    """
    单个RNN-cell 的前向传播过程
    :param x_t: 单元的输入
    :param s_prev: 上一个单元的输入
    :param parameters: 单元中的参数
    :return: s_next, out_pred, cache
    """

    # 获取参数
    U = parameters["U"]
    W = parameters["W"]
    V = parameters["V"]
    ba = parameters["ba"]
    by = parameters["by"]

    # 计算激活函数
    s_next = np.tanh(np.dot(U, x_t) + np.dot(W, s_prev) + ba)
    # 计算当前cell输出预测结果
    out_pred = softmax(np.dot(V, s_next) + by)

    # 存储当前单元的结果
    cache = (s_next, s_prev, x_t, parameters)

    return s_next, out_pred, cache

测试前向过程：假设创建下面形状的数据进行测试，m=3是词的个数，n=5为自定义数字：

UX + WS + ba = S
- [n, m] x [m, 1] +[n, n] x [n, 1] + [n, 1]= [n, 1]
- [5, 3] x [3, 1] + [5, 5] x [5, 1] + [5, 1] = [5, 1]
- U:(5, 3)
- X:(3,1)
- W:(5, 5)
- s:(5, 1)
- ba:(5, 1)
VS + by = out
- [m, n] x [n, 1] + [m, 1]= [m, 1]
- [3, 5] x [5, 1] + [3, 1] = [3, 1]
- V:(3, 5)
- by:(3, 1)

if __name__ == '__main__':
    np.random.seed(1)

    x_t = np.random.randn(3, 1)
    s_prev = np.random.randn(5, 1)
    U = np.random.randn(5, 3)
    W = np.random.randn(5, 5)

    V = np.random.randn(3, 5)
    ba = np.random.randn(5, 1)
    by = np.random.randn(3, 1)
    parameters = {"U": U, "W": W, "V": V, "ba": ba, "by": by}

    s_next, out_pred, cache = rnn_cell_forward(x_t, s_prev, parameters)
    print("s_next = ", s_next)
    print("s_next.shape = ", s_next.shape)
    print("out_pred =", out_pred)
    print("out_pred.shape = ", out_pred.shape)

所有cell的前向传播实现

def rnn_forward(x, s0, parameters):
    """
    对多个Cell的RNN进行前向传播
    :param x: T个时刻的X总输入形状
    :param a0: 隐层第一次输入
    :param parameters: 参数
    :return: s, y, caches
    """
    # 初始化缓存
    caches = []

    # 根据X输入的形状确定cell的个数(3, 1, T)
    # m是词的个数，n为自定义数字：(3, 5)
    m, _, T = x.shape
    # 根据输出
    m, n = parameters["V"].shape

    # 初始化所有cell的S，用于保存所有cell的隐层结果
    # 初始化所有cell的输出y，保存所有输出结果
    s = np.zeros((n, 1, T))
    y = np.zeros((m, 1, T))

    # 初始化第一个输入s_0
    s_next = s0

    # 根据cell的个数循环,并保存每组的
    for t in range(T):
        # 更新每个隐层的输出计算结果，s,o,cache
        s_next, out_pred, cache = rnn_cell_forward(x[:, :, t], s_next, parameters)
        # 保存隐层的输出值s_next
        s[:, :, t] = s_next
        # 保存cell的预测值out_pred
        y[:, :, t] = out_pred
        # 保存每个cell缓存结果
        caches.append(cache)

    return s, y, caches

进行测试

if __name__ == '__main__':
    np.random.seed(1)

    # 定义了4个cell，每个词形状(3, 1)
    x = np.random.randn(3, 1, 4)
    s0 = np.random.randn(5, 1)

    W = np.random.randn(5, 5)
    U = np.random.randn(5, 3)
    V = np.random.randn(3, 5)
    ba = np.random.randn(5, 1)
    by = np.random.randn(3, 1)
    parameters = {"U": U, "W": W, "V": V, "ba": ba, "by": by}

    s, y, caches = rnn_forward(x, s0, parameters)
    print("s = ", s)
    print("s.shape = ", s.shape)
    print("y =", y)
    print("y.shape = ", y.shape)

2、反向传播过
- 单个cell的BP
- 所有cell的BP
单个cell的反向传播

首先根据图中确定需要计算的梯度变量有哪些？

ds_next:表示当前cell的损失对输出 $s^{t}$ 的导数
dtanh:表示当前cell的损失对激活函数的导数
dx_t:表示当前cell的损失对输入x_t的导数
dU:表示当前cell的损失对U的导数
ds_prev:表示当前cell的损失对上一个cell的输入的导数
dW:表示当前cell的损失对W的导数
dba:表示当前cell的损失对dba的导数

def rnn_cell_backward(ds_next, cache):
    """
    对单个cell进行反向传播
    :param ds_next: 当前隐层输出结果相对于损失的导数
    :param cache: 每个cell的缓存
    :return:
    """

    # 获取缓存值
    (s_next, s_prev, x_t, parameters) = cache
    print(type(parameters))

    # 获取参数
    U = parameters["U"]
    W = parameters["W"]
    V = parameters["V"]
    ba = parameters["ba"]
    by = parameters["by"]

    # 计算tanh的梯度通过对s_next
    dtanh = (1 - s_next ** 2) * ds_next

    # 计算U的梯度值
    dx_t = np.dot(U.T, dtanh)

    dU = np.dot(dtanh, x_t.T)

    # 计算W的梯度值
    ds_prev = np.dot(W.T, dtanh)
    dW = np.dot(dtanh, s_prev.T)

    # 计算b的梯度
    dba = np.sum(dtanh, axis=1, keepdims=1)

    # 梯度字典
    gradients = {"dx_t": dx_t, "ds_prev": ds_prev, "dU": dU, "dW": dW, "dba": dba}

    return gradients

多个cell的反向传播

这里我们假设知道了所有时刻相对于损失的的ds梯度值。

测试代码：

    # backward
    np.random.seed(1)

    # 定义了4个cell，每个词形状(3, 1)
    x = np.random.randn(3, 1, 4)
    s0 = np.random.randn(5, 1)

    W = np.random.randn(5, 5)
    U = np.random.randn(5, 3)
    V = np.random.randn(3, 5)
    ba = np.random.randn(5, 1)
    by = np.random.randn(3, 1)
    parameters = {"U": U, "W": W, "V": V, "ba": ba, "by": by}

    s, y, caches = rnn_forward(x, s0, parameters)
    # 随机给一每个4个cell的隐层输出的导数结果（真实需要计算损失的导数）
    ds = np.random.randn(5, 1, 4)

    gradients = rnn_backward(ds, caches)

    print(gradients)

整个网络的反向传播过程

def rnn_backward(ds, caches):
    """
    对给定的一个序列进行RNN的发现反向传播
    :param da:
    :param caches:
    :return:
    """

    # 获取第一个cell的数据,参数，输入输出值
    (s1, s0, x_1, parameters) = caches[0]

    # 获取总共cell的数量以及m和n的值
    n, _, T = ds.shape
    m, _ = x_1.shape

    # 初始化梯度值
    dx = np.zeros((m, 1, T))
    dU = np.zeros((n, m))
    dW = np.zeros((n, n))
    dba = np.zeros((n, 1))
    ds0 = np.zeros((n, 1))
    ds_prevt = np.zeros((n, 1))

    # 循环从后往前进行反向传播
    for t in reversed(range(T)):
        # 根据时间T的s梯度，以及缓存计算当前的cell的反向传播梯度.
        gradients = rnn_cell_backward(ds[:, :, t] + ds_prevt, caches[t])
        # 获取梯度准备进行更新
        dx_t, ds_prevt, dUt, dWt, dbat = gradients["dx_t"], gradients["ds_prev"], gradients["dU"], gradients[
            "dW"], gradients["dba"]
        # 进行每次t时间上的梯度接过相加，作为最终更新的梯度
        dx[:, :, t] = dx_t
        dU += dUt
        dW += dWt
        dba += dbat

    # 最后ds0的输出梯度值
    ds0 = ds_prevt
    # 存储需要更新的梯度到字典当中
    gradients = {"dx": dx, "ds0": ds0, "dU": dU, "dW": dW, "dba": dba}

    return gradients

输出结果

{'dx': array([[[ 6.07961714e-02,  6.51523342e-02,  1.35284158e-02,
         -4.17389120e-01]],

       [[-1.87655227e-01,  1.88161638e-01,  2.76636979e-02,
          5.88910236e-01]],

       [[-2.10309856e-01,  1.17512701e-01, -1.81722854e-05,
          1.33762936e+00]]]), 'ds0': array([[-0.04446273],
       [-0.48089235],
       [-0.20806299],
       [ 0.05651028],
       [ 0.24527145]]), 'dU': array([[-7.75341202e-02,  1.14056089e-03, -1.39468435e-01],
       [-3.76126305e-01, -2.71092586e-01, -7.68534819e-01],
       [-2.27890773e-01, -4.52402940e-01, -5.62591790e-02],
       [ 3.67591208e-02,  1.45958528e-01,  1.47219164e-02],
       [-1.16043009e+00, -8.51763028e-01, -1.44090680e+00]]), 'dW': array([[ 0.04560171,  0.04695379,  0.0257273 , -0.02726464,  0.05504417],
       [ 0.37031535,  0.3703334 ,  0.38913814, -0.39608747,  0.36938758],
       [ 0.21223499,  0.3431846 ,  0.22255773, -0.35298064,  0.21136843],
       [-0.06210387, -0.06084794, -0.06470341,  0.06497274, -0.03480747],
       [ 0.78119033,  0.74650186,  0.34013264, -0.31155225,  0.6784628 ]]), 'dba': array([[ 0.02851001],
       [ 0.39449393],
       [ 0.35633039],
       [-0.06492795],
       [ 0.33991813]])}

那么接下来，我们看看RNN的一些改进结构，这里大家只要了解相关结构以及作用即可，不需要会公式的推导等。

4.1.4 GRU(门控循环单元)

2014年，

4.1.4.1 什么是GRU

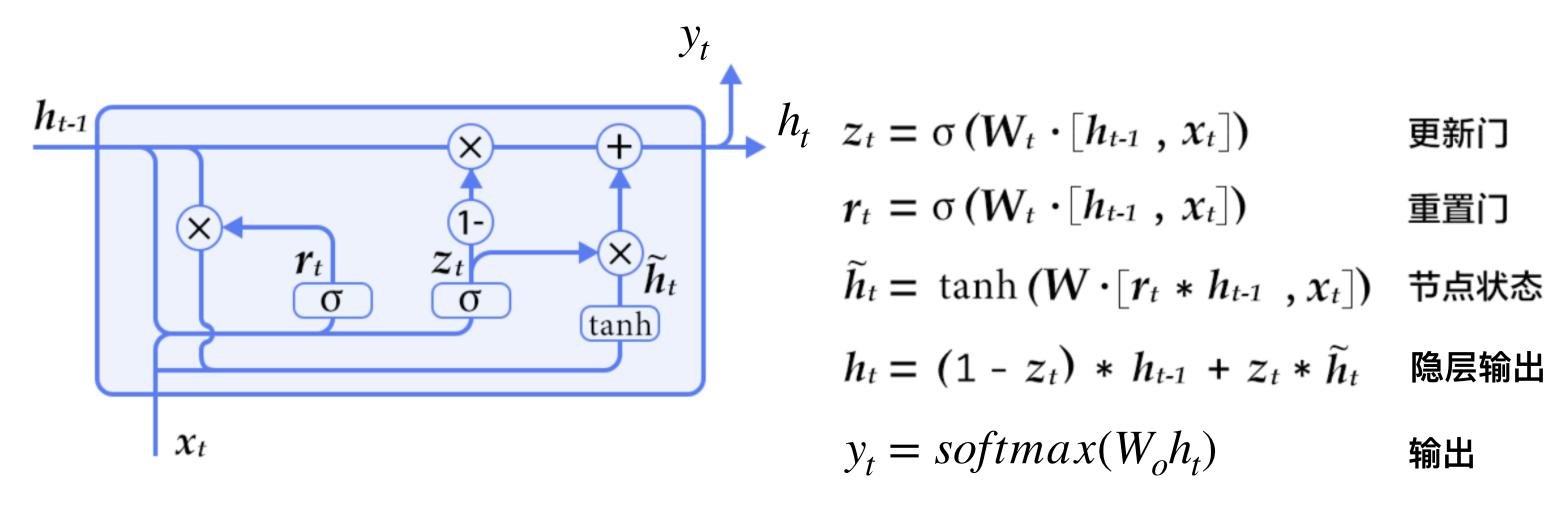
GRU增加了两个门，一个重置门（reset gate）和一个更新门（update gate）
- 重置门决定了如何将新的输入信息与前面的记忆相结合
- 更新门定义了前面记忆保存到当前时间步的量
- 如果将重置门设置为 1，更新门设置为 0，那么将再次获得标准 RNN 模型

4.1.4.2 直观理解

The cat,which already ate,…….,was full.

对于上面的句子，was是句子前面的cat来进行指定的，如果是复数将是were。所以之前的RNN当中的细胞单元没有这个功能，GRU当中加入更新门，在cat的位置置位1，一直保留到was时候。

4.1.4.3 本质解决问题

原论文中这样介绍：

为了解决短期记忆问题，每个递归单元能够自适应捕捉不同尺度的依赖关系
解决梯度消失的问题，在隐层输出的地方 $h_t,h_{t-1}$ 的关系用加法而不是RNN当中乘法+激活函数

4.1.5 LSTM(长短记忆网络)

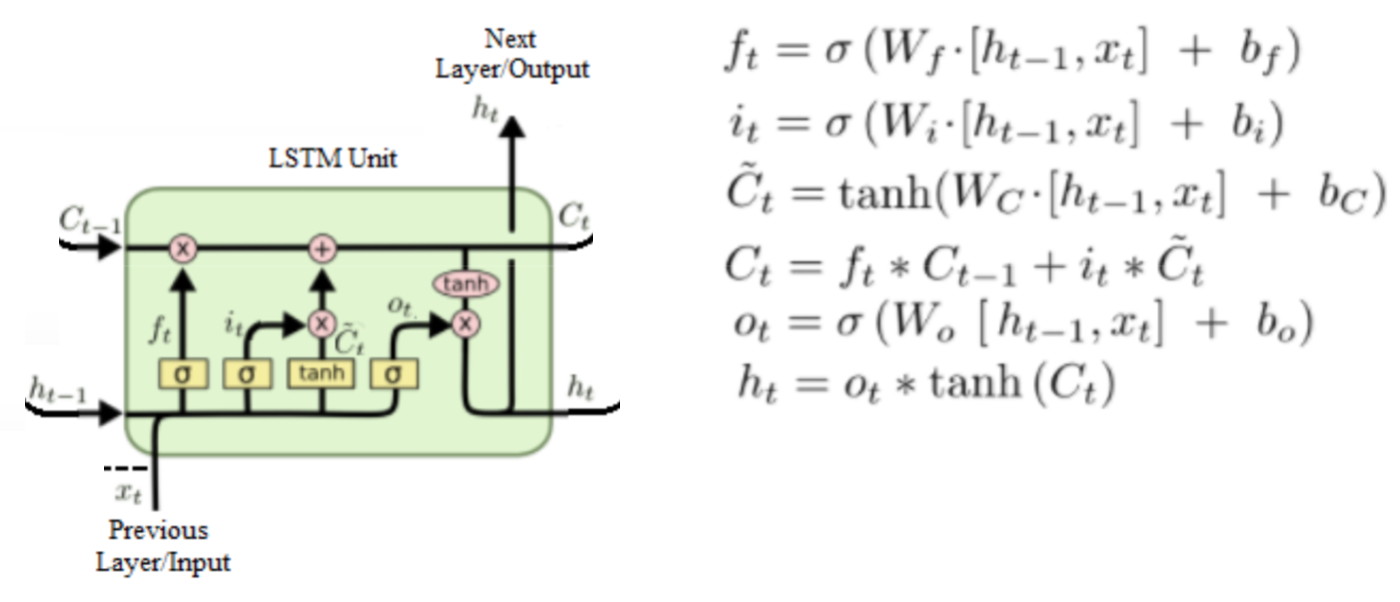
$h_t$ :为该cell单元的输出
$c_t$ :为隐层的状态
三个门：遗忘门f、更新门u、输出门o

4.1.5.1 作用

便于记忆更长距离的时间状态。

4.1.6 总结

掌握循环神经网络模型的种类及场景
掌握循环神经网络原理
- 输入词的表示
- 交叉熵损失
- 前向传播与反向传播过程